Before you start reading, If you are not familiar with NARDL see A Quick Explanation of Recent NARDL where i formulated a food import model (for India for the illustration purpose). In this post, i estimated the NARDL model with Eviews 8/9. The raw data used to demonstrate with Eviews can be downloaded from google drive. Download Workfile. Or send a hi to my Email: hssanhanif@gmail.com or meet me at dept. of Economics and Banking, IIUC. This file contains the yearly data of inflation rate and ''percentage of food import to total import'' of India . The food model has the following form:
Foodt=C+ INFt+Ut
Where, Foodt indicates % of Food Import of total import. (dependent variable) and INFt indicates inflation rate (independent variable).
Since NARDL is a recently developed model, Eviews 8, Eviews 9 or other current versions do not have any built-in option yet to estimate NARDL. So,
Follow these steps:
F
Follow these steps:
F
Step 1. Perform unit root tests to make sure that non of the variables are I(2).
|
Step 2. Generate INFt+ and INFt– from INFt
|
Step 3. Run the Non linear ECM under NARDL
|
Step 4. Test the ‘non linear cointegration’ test with F-test
|
Step 5. check the asymmetries.
|
Step1: run unit root test to make sure that data are not I(2).
Like the ARDL error correction model by pesaran et al (2001), the NARDL does not allow I(2) variables. To perform unit root test in Eviews: ⟾click on the series unit root test ⟾select level and ⟾select intercept and trend now see the p-value. If it is less than 0.05 the series is said to be ststionary or I(0) at 5% significance level. and if not repeat the steps and this time select the choice first difference. If p-value is less than 0.05 then series is said to be stationary at first difference or I(1). And if it is more than 0.05 the series is not I(1). And should not be entered in NARDL model. I have checked each series and found that Foodt is integrated of order 1 or I(1) and inflation is found to be the integrated of order zero I(0). So we can run NARDL. You can verify the order of integration with the Eviews workfile i provided in first paragraph.
Step 2 Calculate partial sum of positive and negative change:
To do this, copy each line of the commands given in the box paste it into the command area of Eviews then press ENTER in keyboard. For example after putting genr dinf = inf-inf(-1) press ENTER than put the 2nd line genr dfood=food-food(-1) then press ENTER and so on. To understand these commands, what these commands to is that they create first difference variable of inf and food: dinf and dfood, then create a series for the values of dinf which are not negative and another series for negatives. Then they calculate the cumulative sum of each after multiplying positive and negative series by the first difference. The resulting cumulative sums are partial sum of positive and negative changes in inflation, which denoted by inf_p and inf_n, respectively.
Eviews Commands to decompose independent variable in NARDL.
Note: throughout this Eviews illustration, INFt+ is denoted by inf_p and INFt– denoted by inf_n |
genr dfood=food-food(-1)
genr dinf = inf-inf(-1)
genr pos = dinf >=0
genr dinf_p = pos*dinf
genr dinf_n = (1-pos)*dinf
genr inf_p = @cumsum(dinf_p)
genr inf_n = @cumsum(dinf_n)
|
Step 3: Run the Non linear ECM under NARDL
Step 3.1 Estimating NECM under NARDL framework
Now ⟾ click on quick estimate equation ⟾ choose two steps least square from drop down list and specify the equations in both of the boxes as shown the picture below.
d(food) c food(-1) inf_p(-1)
inf_n(-1)
dfood(-1 to -4) dinf_p(-0 to
-4) dinf_n(-0 to -4)
|
 |
| NARDL specification |
Explanation of the specification: The specifications in first box contains the dependent variable d(food), constant C, followed by 3 independent variables—the first lagged term of food: food(-1), the first lagged term of partial sum of positive change in inf which is denoted by inf_p(-1), and the first lagged term of partial sum of negative change in inf which is denoted by inf_n(-1). The second box contains the set of differenced variables upto 4 lags. ( i chose maximum lag 4 since the data are yearly). By specifying (-1 to -4), all the lagged terms of dfood from first lag to fourth lag are included. So as for the rest. 0 lag implies no lag. The 0 lag of Xt, for example, is the Xt itself. Note here that the 0 lag is not included in case of dfood because dfood is already acting as dependet variable in the model.
But, before you click OK, click ‘options’ and set the settings as shown in the picture below
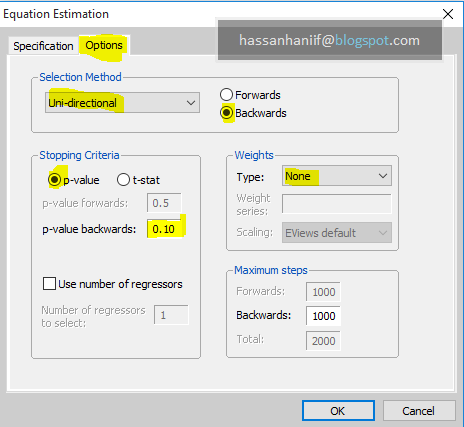 |
| This setting will drop the insignificant stationary variables from NARDL model as suggested by Shin et al (2014) |
Choose unidirectional, backwards, p-values, set p-value 0.10 (or 0.05 or even 0.01.) I chose 0.10 here. Also choose uni directional and backwards. The interpretation of this setting is that it will remove the variables that are not significat even at 10% level while it will retain the variables of upper panel of the box even if they are not significant this was chosen in shin' study. However, this setting is not hard and fast rule. The goal is to select the appropriate model specification with appropriate lags for the differenced regressors. You can choose other criteria to choose appropriate lags.
3.B NARDL output, long-run coefficients and interpretation:
By a quick glance to the output we can learn that Eviews removed some lags and that 0.308099 and 0.390456 are the coefficients of inf_p and inf_n, respectively. But they are not the long run coefficient. To calculate the long run coefficient divide the negative of coefficient of each inf_p and inf_n by the coiefficient of food(-1). So the long run coefficient of inf_p is -0.0308099 /-0.457567=0.673342 and long run coefficient of inf_n is -0.390456/-0.457567=0.853331 . clearly, both long-run coefficient are positive. hence So the long run equation or the cointegrating equation is :
long run equation: 🔴 Food= 0.673342inf_p + 0.853331inf_n +u
interpretation of NARDL output: 1 percent point increase in inflation rate leads to 0.67 percent point increase in food import India (positive realtion), and 1 percent point decrease in inflation rate leads to 0.85 percent point decrease in food import (also positive relation). (I said percent point because the variables are rates) clearly, the food import response more to negative change because the coefficient is larger.
After clicking OK you will see Wald test results as shown in the picture below.
interpretation of NARDL output: 1 percent point increase in inflation rate leads to 0.67 percent point increase in food import India (positive realtion), and 1 percent point decrease in inflation rate leads to 0.85 percent point decrease in food import (also positive relation). (I said percent point because the variables are rates) clearly, the food import response more to negative change because the coefficient is larger.
Step 4: Asymmetric Cointegration test:
Before drawing any conclusion regarding the estimated coefficients one needs to check if variables are co-inetgrated. The coefficients would be sporious if variables are not cointegrated. For testing cointegration under NARDL, Shin at al recommended to use joint null hypothesis of level (non-diffrenced) variables and to compare the critical values of bound testing in pesran et al (2001). (You can download the paper from internet, and find the table in Page 300). If the calculated F statistics is found to be the greater than the upper critical value then there is evidence of co-integration. And if not, then evidence of cointegration is not found.
To start cointegration test in Eviews click view on output window⟾coefficient diagonistics⟾wald test-coefficient restriction. ⟾Specify the restriction c(2)=c(3)=c(4)=0. Then click OK’. Clearly, this wald test perform the joint null hypothesis of the coefficient of food(-1) which is second coefficient in the list (hence the notation c(2)), and the coefficient of lnf_p which is c(3) and and the coefficient of inf_n which is c(4). Basically, this joint null hypothesis acts as the null hypothesis of no cointegration. The procedure is illustrated in the picture below.
 |
| Asymmetric cointegration test under NARDL |
After clicking OK you will see Wald test results as shown in the picture below.
 |
| The calculated F-statistics for this (asymmetric) cointegration test |
The calculated F-statistics is 13.34022. now lets compare it with critical values of
pesaran et al (2001). Here is the screenshot. Of case III.
 |
| Pesaran et al. (2001) critical values Case III. |
Case III was chosen because in the NARDL representation on my food model there is a constant.(intercept was not restricted). In the table, k denotes the number of long run regressors. Note here that there are two independent variables in long run equation of my food model :inf_p and inf_n. but I chose k=1. The reason is that, the variables actually came from from 1 variable, hence, the k lies between 1 and 2. Also notice in table that the critical value for small k is larger. If the null hypothesis of no cointegration is rejected by critical value of its smaller k, then according to shin et al(2014) there is a strong evidence of co-integration. In my food model i chose k=1, but for large number of variables set k equal to number of regressors before decomposition.
Decision: since The calculated F statisics is larger than The crticical value 7.84 at 1% significance level, there is strong evidence of cointegration at 1% significance level.
Eviews will show the wald-test results as in the picture below.
I'm thankful to M.J. Greenwood-Nimmo, one of the author of Shin et al (2014), and to Rizgar Abdlkarim, co-author "Oil and Food Prices Co-integration Nexus for Indonesia: A Nonlinear ARDL Analysis." International Journal of Energy Economics and Policy 6.1 (2016).
Step 5. Testing the presence of asymmetry:
both of the positive change and the negative change have the long-run positive effect on food import. But are they really (statically) different ? an asymmetry test basically test if the coefficient are equal or not. If they are equal then threre is no asymmetry and if they are not then threre is evidence of asymmetry. Recall from step 3 .2 that we calculated long run coefiicient for inf_p and inf_n by –c(3)/c(2) and –c(4)/c(2), respectively. So, To test the long run asymmetry in Eviews click on wald test and write this command below in the restriction box of wald-test.
–c(3)/c(2)=–c(4)/c(2)
|
Eviews will show the wald-test results as in the picture below.
 |
| Wald test results for asymmetry test. |
Decision: Clearly, the null of hypothesis of equality is rejected as p-value is less than 0.05. Wald test indicates that there is asymmetry in the long run impact of inflation on food import in India.
The Last step:
Check the robustness by various diagnostic tests. I will not explain theme here but I saved the results of what I have shown above including the results of diagnostic tests. If you are stuck please do not hesitate to ask me.
Important Note: This is not a full fledged research, rather an illustration to show how to estimate NARDL. This model may suffer from omitted variable bias or any type of model misspecification, I'm not claiming that these results are valid for India.
Acknowledgement:
Important Note: This is not a full fledged research, rather an illustration to show how to estimate NARDL. This model may suffer from omitted variable bias or any type of model misspecification, I'm not claiming that these results are valid for India.
Acknowledgement:
I'm thankful to M.J. Greenwood-Nimmo, one of the author of Shin et al (2014), and to Rizgar Abdlkarim, co-author "Oil and Food Prices Co-integration Nexus for Indonesia: A Nonlinear ARDL Analysis." International Journal of Energy Economics and Policy 6.1 (2016).





what if we have more than one exogenous variables, given we added the variable A . how to modify the following code
ReplyDeletegenr dfood=food-food(-1)
genr dinf = inf-inf(-1)
genr pos = dinf >=0
genr dinf_p = pos*dinf
genr dinf_n = (1-pos)*dinf
genr inf_p = @cumsum(dinf_p)
genr inf_n = @cumsum(dinf_n)
Hi Mr. Hssaine,
Deletereplace the inf by the exogenous variable and run the code again. say we added the variable Z then,
genr dZ = Z-Z(-1)
genr pos = dZ >=0
genr dZ_p = pos*dZ
genr dZ_n = (1-pos)*dZ
genr Z_p = @cumsum(dZ_p)
genr Z_n = @cumsum(dZ_n)
best regards,
Hassan
thank you sir. So if we have 2 exogenous variables, the code can be written as :
Deletegenr dfood=food-food(-1)
genr dinf = inf-inf(-1)
genr pos = dinf >=0
genr dinf_p = pos*dinf
genr dinf_n = (1-pos)*dinf
genr inf_p = @cumsum(dinf_p)
genr inf_n = @cumsum(dinf_n)
genr dZ = Z-Z(-1)
genr pos = dZ >=0
genr dZ_p = pos*dZ
genr dZ_n = (1-pos)*dZ
genr Z_p = @cumsum(dZ_p)
genr Z_n = @cumsum(dZ_n)
yes !
DeleteDear sir,
DeleteI had also the same doubt. Thank you so much for the doubt clarification. I have one more doubt: I have more than 2 explanatory variable. So, should i use the above mentioned code for every explanatory variable or only for the explanatory which i believe that it has asymmetric relationship with the dependent variable?
Thank you!
thank you sir, I appreciate your help
ReplyDeleteyou are welcome, sir
DeleteDear Prof,
ReplyDeleteHow to calculate short run asymmetry?
Dear aim84, i think, you can notice the short-run symmetry or asymmetry for each of the 'laggaed differenced regressors' by looking at the results. For instance, DINF_P(-3) has a significant coefficient but DINF_N(-3) is absent from the table (due to its insignificant coefficient) implying an asymmetry.
DeleteDear Scravs,
ReplyDeleteI do not think so. And it was advised to remove insignificant stationary regressors ( i. e the differenced terms).
Prof., with hope you are fine,My name is Muftau a faculty member Department of Economics usmanu Danfodiyo University, Nigeria
ReplyDeleteProf, what if we have more than one exogenous variables say four variables but am interested in testing asymmetry for only one exogenous variable do we still have to calculate partial sum of positive and negative change for all exogenous variables (decompose all independent variables) or just for the variable of interest
Dear Olarinde Muftaw,
DeleteDecomposing all the exogenous variables is not necessary.
This paper may help you
http://www.sciencedirect.com/science/article/pii/S1059056016301939
http://dx.doi.org/10.1016/j.iref.2017.02.007
You are welcome.
ReplyDeleteYou're welcome.
ReplyDeletedear Sir, how I get multiplier impact ?
ReplyDeleteThank you very much for your knowledge, prof. It is so helpful to me. I want to ask you, how i get the curve of dynamic effects between dependent and independent variable? And i ever red about the analysis of the short run dynamics with wald test, how can i get the short run dynamics? to make sure in the short run, there is symmetric adjustment
ReplyDeleteDear Sir
ReplyDeleteI am done with the asymmetries effect in the NARDL model. I need to know "how to run the dynamic multiplier" effect in the model.
Regards
Akhil Sharma
This comment has been removed by the author.
ReplyDeleteI am little confused about this anylysis first of u checked ur bound test results at the significant level of %10 but asymetric checking in %5 also is your data in a logarithmic form because of ur comments about coeficints with percent and if our asymetric test results shows us there is no asymetri in our model we cant apply nardl is it right ? thanks for your useful blog
ReplyDeleteplz how to run the dynamic multiplier ?
ReplyDeletehello, really great job i have question , why you put lag -4 in equation this dfood(-1 to -4) dinf_p(-0 to -4) dinf_n(-0 to -4)
ReplyDeletethank you very much
The selective removal of stationary regressors is logical but Eview 9 ARDL option does not do that. May be there is a reason for that.What you are suggesting is the General to Specific Procedure. I personally like it but...... please shed some more light on this so that there is no objection if I sen it for publishing.
ReplyDeletehello sir
ReplyDeleteif we have two exogenous variables and we want to decompose just one of them into partial sum how to specify the equations in both of boxes of tow steps least square ? to be more specific if we have this equation : inflation=b0+B1realgdp+B2oil price+µt
and we want to decompose oil price into partial sums so how do we write the commands for the partial sums and how do we specify the tow equations in both of boxes of tow steps least square ? knowing that each of inflation, realgdp and oilp are I(1) I hope you answer my question sir
This comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteError Correction Model (ECM) Panel Data EVIEWS 9
ReplyDeletehttps://www.youtube.com/watch?v=ZgCwrb6kI7w
video Introduce the concept of an Error Correction Model (ECM) Panel Data EVIEWS 9.
WhatsApp : +6285227746673
PIN BB : D04EBECB
IG : @olahdatasemarang
hi again
ReplyDeleteplease help me why you chose k=1 when you did compare with F , for cointergration
thank you very much
Dear Professor: How do I use the results to know the short-term relationship؟
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThank you for this detailed breakdown on NARDL test for Asymmetry. It addresses the issue I am currently grappling with. I am using Eviews 9 Student Version and estimating the LR and SR versions of the ECM equation is a single step. My problem is that I get several lags of the dependent variable. For example in your case you got just FOOD (-1). I often get FOOD (-1), FOOD (-2)... So which of these do I use the coefficient needed in the denominator for the Wald Long run test? Thanks in advance for your help.
ReplyDeleteIn your code below, what is the purpose of this line:genr dinf_p = pos*dinf and the next line that uses (1-pos)? You seem to be multiplying the positive first difference with the first difference at every time step. why is that done? I would think the goal of the lines of code is to generate 2 series: a cumulative sum of the positive and negative first differences.
ReplyDeletegenr dfood=food-food(-1)
genr dinf = inf-inf(-1)
genr pos = dinf >=0
genr dinf_p = pos*dinf
genr dinf_n = (1-pos)*dinf
genr inf_p = @cumsum(dinf_p)
genr inf_n = @cumsum(dinf_n)
Great. Good Job dear.
ReplyDeleteCan you please explain Non-linear (Asymmetric) causality developed by Hatimi (2012)??
This comment has been removed by the author.
ReplyDeleteNARDL add-in is officially out on the Eviews add-in page. It allows you to also compute dynamic multiplier as well as cusum and cusumsq.
ReplyDeleteNARDL add-in is officially out on the Eviews add-in page. It allows you to also compute dynamic multiplier as well as cusum and cusumsq.
ReplyDeletehello dear sir.my question is if we have more than one independent variable and we want to decompose only one independent variable then how will we represent our model in equation form then
DeleteNARDL addin is officially available on Eviews add-in page.
ReplyDeleteGreat job! I would like to ask how to plot the asymmetric cumulative dynamic multiplier. Thanks
ReplyDeleteIt is very useful to apply the NARDL Model.
ReplyDeleteDear sir
ReplyDeleteThank you very much for nice discussion. Can you please suggest me how can I get symmetric and asymmetric series of the dependent variable after the analysis?
Thanks
Chhiddikur
This comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeletehi.
ReplyDeleteI neead your help for Interpretation of the sign of short-run long run coefficients. why the sing oil negative oil is positive?
and how can count the short run coff?
thansk a lot
dears, can you tell me the command for NARDL for panel data. It says syntax error
ReplyDeletehow many regressor we can thake at a time
ReplyDeleteAoa
ReplyDeleteThank you for a very helpful post indeeed
What about short run results?
This comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThis comment has been removed by the author.
ReplyDeletethank you professor for your great post. i run a nardl model and my results show that there is cointegration, but my long run coefficients are not significant. is it meaningful to calculate long run coefficients with –c(3)/c(2) and –c(4)/c(2) ?
ReplyDeleteHi;
ReplyDeletehow to use the bootstrap to perform these NARDL steps please?
Dear Professor, with hope you are fine, My name is Feiyun Xiang.
ReplyDeleteProf, what if we have two exogenous variables but we are interested in testing long-run and short-run asymmetry for one exogenous variable, and we are interested in testing only short-run asymmetry for another exogenous variable? Can we do these tests in one equation?
Thanks in advance for your help.
i have hetero and serial correlation in the model how what i do even i transformed my variables into log for
ReplyDeleteThank you sir for this step-by-step guidance 🙏
ReplyDeleteTHANKS A LOT, BUT I WANT TO ASK IF I CAN FIND THE THRESHOLD FOR INF THROUGH NARDL. THANKS A LOT AGAIN.
ReplyDeleteThanks a lot!
ReplyDeleteAutoRegressive Distributed Lag (ARDL) Data Panel Eviews 12
ReplyDeletehttps://dik.si/ARDL12
ECM (Error Correction Model) Panel Data Eviews 12
ReplyDeleteEstimating Error Correction Model (ECM) with Eviews 12 (Panel Data)
Visit
https://dik.si/ECMPD
Hi professor, I use your way and get every result but I ma wonder how to get the ecm coefficient?
ReplyDeletePortable EViews 13 Crack Full Version
ReplyDeleteClick
Download Portable EViews 13 Crack Full Version
Portable STATA 18 Crack Full Version
ReplyDeleteSTATA 18 Crack Full Version
STATA 18 Full Version
Link Download STATA 18 Full Version
https://rutube.ru/video/2eab69d75044eb5856998125e0e71a93